CNN, RNN이 무엇인지 간단하게 알아보자
CNN
CNN은 Convolutional nueral network의 약자로 인공신경망의 한 종류이다. 이를 위해하기 위해서는 먼저 Convolution과 활성함수에 대해 이해해야한다.
Convolution
Convolution은 kernel을 입력벡터상에서 움직여가며 선형모델과 합성함수가 적용되는 구조이다. 이렇게 말하면 감이 안오니 그림으로 보자.

밑의 파란색 데이터가 입력값, 움직이는 3 x 3 구역이 kernel, 위의 초록색 데이터가 출력값이다.
입력데이터를 kernel이 움직이면서 kernel과 입력데이터가 합성되고, 그 결과값을 출력값에 넣고 있는것이다.
어떤 연산이 이루어지는지 한번 보자.

위 예시의 kernel은 3 x 3 행렬로 \( \begin{bmatrix}
0 & 1 & 2 \\
2 & 2 & 0 \\
0 & 1 & 2 \\
\end{bmatrix} \)값을 가진다. 출력값의 계산은 행렬곱을 이용해 계산된다.
즉, 첫번째 칸의 출력값 12는 \(3\times 0 + 3\times 1 + 2\times 2 + 0\times 2 + 0\times 2 + 1\times 0 + 3\times 0 + 1\times 1 + 2\times 2 = 12 \) 의 계산결과인 것이다.
위의 예시는 2D convolution인데, 3차원 이상의 공간에서도 convolution이 가능하며, 입력이 d차원인 경우 kernel 또한 d차원의 kernel이어야 하고, convolution의 결과는 2차원으로 나온다. 결과값이 3차원 값을 갖게 하려면 kernal의 갯수를 늘리면 되고, kernal이 n개면 결과값 또한 n개의 2차원 matrix로 출력된다.
활성함수 (Activation Function)
활성함수는 실수 2차원 평면 위에 정의된 비선형 함수로, 지금은 딥러닝 신경망을 구성하는데 있어서 딥러닝 모델과 선형모델을 구분짓는 중요한 함수라고만 말하자. 대표적인 활성함수로는 sigmoid, tanh, ReLU 등의 함수가 있다.

CNN은 이런 Convolution 신경망과 활성함수(Activation function)의 그물로 이루어져있다. 쉽게말해
Convolution - 활성함수 -Convolution - 활성함수 - ... 처럼 이어져있다 볼 수 있다.
이렇게 신경망을 구축했다면 마지막으로 인공신경망을 구성하는 또다른 중요한 요소 역전파(backpropagation)을 해줘야 한다.
역전파(Backpropagation)
역전파는 깊은 층부터 gradient를 계산해 그 전 층으로 미분값을 전달하는 것으로, 모델이 계산을 할때 깊은 층의 계산 정보가 필요하기 때문에 하는 작업이다.
각각의 가중치 행렬에 대해 손실 함수에 대한 미분을 해주고, 각 층의 paremeter에 gradient vector를 계산하여 더 얕은 층으로 전달하는 방식으로 가중치들을 갱신해준다.
CNN의 경우에는 이런 역전파를 출력값에서 입력값으로, 그리고 출력값에서 kernel로 시행해줘야 한다.

입력값으로의 역전파의 경우 전달받은 gradient값들에 출력값의 각 값들을 곱해 더한 값이 전달되게 된다.

kernel로의 역전파의 경우 전달받은 전달받은 gradient의 tuple에 입력값의 값을 곱하는 방식으로 역전파 값이 전달된다.
이렇게 되면 우리는 CNN의 간략한 구성에 대해 이해했다고 할 수 있다.
RNN
RNN은 Recurrent Neural Network의 약자로, 연속적인 데이터의 처리를 위해 고안된 인공신경망이다.
문장, 비디오, 주가 등 연속적이 값들은 독립동등분포 가정을 위배하기 때문에 그 순서를 바꾸거나 그 전 값의 정보가 없다면 데이터를 잘못 이해하기 쉽다. 따라서 이러한 sequence data를 다루기 위해 고안된 신경망이 RNN이다.
이전값들을 기반으로 다음 값을 해석하기 위한 모델을 구축하는데, sequence data의 특성상 데이터의 길이가 가변적이다. 이를 해결하기 위해 다음처럼 이전값들을 하나의 값으로 묶어 점화식처럼 2개의 입력을 받는 연속적인 함수를 고안할 수 있다.

위의 함수를 바탕으로 아래와 같은 연속적인 신경망을 구성할 수 있다. X가 입력값, H가 이전변수들이 종합된 변수, O가 해당 단계의 출력값이다.
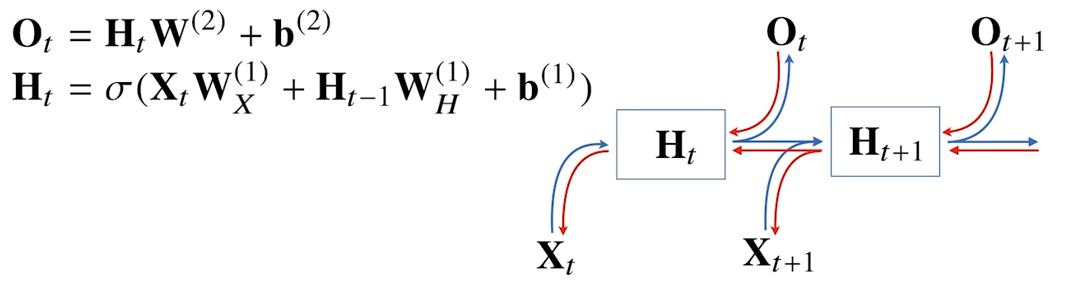
RNN 또한 역전파를 구현해줘야한다. RNN은 출력값에서 해당 단계의 변수로, 그리고 다음 단계의 변수에서 이전단계의 변수로 전달되는 두개의 역전파를 가지고 있다.
RNN은 모델의 특성상 전달되는 gradient들이 계속 곱해지게 되는데, 이를 Backpropagation Through Time(BPTT)라 한다.
이런 특성때문에, 모델이 커질경우, gradient값이 1보다 크면 무한대로, gradient 값이 1보다 작으면 0으로 향하는 현상이 발생하게 된다. 특히, 0으로 향할 경우 기울기 소실(gradient vanishing)이 발생해 모델 학습에 문제가 생길 수 있다. 따라서 특정 지점에서는 역전파를 끊어줄 필요가 있다.
이렇게 역전파를 끊어주는 것을 truncated BPTT라 하고, 역전파가 끊어진 지점에서는 출력값에서만 gradient를 전달받게 된다.
이렇게 Vanilla RNN의 기울기 소실때문에 발생하는 문제를 해결하기 위해서 등장한 모델들이 GRU와 LSTM인데, 이들에 대해서는 다음에 알아보도록 하자.