여러 Optimization 기법에 대해 알아보자

이번 포스팅에서는 optimizer에 대해 알아보고자 한다.

먼저 optimization에 관한 핵심 개념들에 대해 알아본 후 실제 사용되는 optimzer들에는 어떤 것들이 있는지 알아본 후, Regularization에 대해 알아볼 것이다.

 

1. gradient descent

목적식의 미분값을 이용해 함수의 local minimum을 향해 가는 것을 의미한다. 경사하강법에 관해 설명한 포스팅이 있으니 잘 모르겠다면 보고 오자

https://roki9914.tistory.com/4

경사하강법과 선형회귀

2. Underfitting, Overfitting, Generalization

이 세 개념은 한번에 보는 것이 좋다.

먼저 underfitting은 training이 너무 안된 것으로 일반적으로 train 데이터에서의 정확도조차 좋지 않게 나왔을 때 underfitting인 상황이라고 한다.

overfitting은 이와 반대되는 상황이다. 모델이 train 데이터를 너무 잘 학습한 상황인 것이다. "잘 학습했다면 좋은것이 아니냐?" 라고 말할 수 있지만 이는 좋지 않은 상황이다. 왜냐하면 train 데이터를 너무 잘 학습한 나머지 train 데이터가 아닌 처음보는 데이터에 대해서는 정확도가 좋지 않게 나오기 때문이다. 딥러닝의 목적이 train 데이터를 이용해 처음 보는 데이터에 적용하는 것이라는 걸 생각해보면 overfitting된 모델은 사용할 수 없게 된다.

Generalization이란 개념은 이런 상황에서 나온 것이다. Generalization은 처음보는 데이터에 모델이 얼마나 잘 적용되는지를 나타내는 개념으로 training error와 test error 의 차이를 generalization gap이라고 한다.

따라서 우리는 아래 그림과 같이 underfitting도 아니고 overfitting도 아닌 딱 적절하게 학습된, generalization gap이 가장 작은 지점까지 모델을 학습하는 것이 목표라고 할 수 있다.

3. Cross-Validation (aka. k-fold validation)

Cross-Validation은 train 데이터의 일부를 validation 데이터로 분리시켜 학습된 모델이 처음보는 데이터에 얼마나 잘 적용되는 지를 예측하는 것을 말한다. "그냥 test 데이터로 확인해보면 되는거 아니냐?"라고 할 수 있지만, 모델을 학습하는 데 있어서 어떤 경우에도 test 데이터를 사용하지 않는 것이 원칙이기 때문에 일부러 train data를 쪼개 validation data를 만드는 것이다.

또한, validation data를 제외한 train data도 여러개로 쪼개 각각에 대해 cross-validation을 시행할 수도 있는데, 이를 통해 모델을 학습하는데 있어서 최적의 hyperparameter를 찾는데 이용할 수도 있다. 이렇게 각각 쪼개진 train data를 fold라 하고, 여러개의 fold를 사용하는 validation이라 하여 k-fold validation이라고 부르기도 한다.

4. Bias and Variance

Bias와 Variance의 개념 자체는 간단한다. 단어 뜻 그대로 bias는 전체적으로 데이터가 중점에서 치우친 정도를 말하고 variance는 데이터가 퍼져있는 정도를 말한다. 아래의 그림을 보면 이해가 쉬울 것이다.

딥러닝에서의 bias는 알고리즘상에서 잘못된 가정을 했을 때 발생하는 오차를 말하고, variance는 train data에 내제된 작은 변동에 의해 발생하는 오차를 말한다. 

이때 bias and variance tradeoff이라는 개념이 등장한다. 우리는 모델을 학습시킬 때 학습 알고리즘의 기대 오차를 줄이기 위해 노력하는데, 이때 오차는 bias, variance, noise(데이터 자체에 포함된 오차)로 구성된다. 이때 다음과 같은 식이 구성된다.

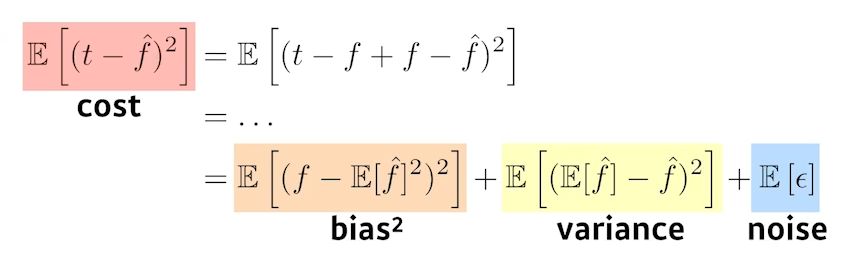
위의 식에서 볼 수 있든 세 요소가 서로 더해지는 형태를 취하기 때문에, bias를 줄이면 variance가 늘어나는 경향을 보이고, 반대로 variance를 줄이면 bias가 늘어나는 경향을 보인다. 이를 우리는 bias-variance tradeoff이라 한다. 

 

5. Bootstrapping

Bootstrapping은 하나의 dataset으로 하나의 모델을 만드는 것이 아닌, random sampling을 통해 하나의 dataset에서 여러개의 작은 dataset을 만들고, 각각의 data로 모델을 학습시키는 것을 말한다. 이렇게 여러개로 학습된 모델을 이용하여 각 모델이 같은 입력에 대해 일치하는 정도를 볼 수 있으며, 모델이 얼마나 안정적인지를 확인할 수 있다.

 

6. Bagging & Boosting

Bagging은 bootstrapping aggregating의 약자로, bootstrapping으로 만든 여러 모델의 출력을 aggregate하는 것을 의미하고, Boosting은 모델을 처음 학습시켰을 때, 해당 모델이 잘 분류하지 못한 데이터들을 이용해 따로 모델을 만들고, 이렇게 만들어진 모델들을 합치는 것을 의미한다. 이를 weak learner들이 모여 strong learner가 된다고 표현하기도 한다.

 

마지막으로 본론에 들어가기에 앞서 먼저 여러 gradient descent methods들과, batch의 사이즈와 대해 간단히 알아보자. 경사하강법의 method에는 크게 3가지가 있다: SGD, mini-batch gradient descent, batch gradient descent.

SGD는 우리가 흔히 그런 의미로 쓰진 않지만, 엄밀하게 의미를 따지자면 data를 크기가 1인 batch로 나눠 경사하강법을 적용하는 것을 말한다.

Mini-batch gradient descent는 그보다는 큰 batch를 사용하는 방법으로 이것이 우리가 흔히 SGD라고 부르는 확률적 경사하강법이며, 대부분의 학습에서 채용하는 방법이다.

Batch gradient descent는 data를 batch로 나누지 않고 한번에 전부 적용시키는 것을 말한다.

학습할 때 batch의 크기가 작아질수록 학습 효율이 좋아지는데, 이는 수학적으로 증명된것이라기 보다는 여러번의 실험을 통해 통계적으로 봤을 때, batch size가 작아질수록 flat minimizer로 수렴하고, batch size가 커질수록 sharp minimizer로 수렴하는 것을 확인한 것이다. Flat minimizer와 sharp minimizer는 아래와 같은 함수를 말한다.

 위의 그림을 보면 flat minimizer의 경우 x축의 input이 조금 달라도 training function과 testing function의 y의 output이 크게 다르지 않은것을 볼 수 있다. 그러나, sharp minimizer의 경우 input이 조금만 달라져도 output의 차이가 커지는 것을 볼 수 있다. 따라서, flat minimizer인 경우, 즉 batch의 크기가 작을수록 generalization gap이 줄고, generalization이 잘 된다는 것을 알 수 있다. 다만, 이에 입각하여 우리가 batch의 크기를 1로 하지 않는것은, 시간이 너무 오래 걸리기 때문이다. 

지금까지 optimization에 대해 알아보기에 앞서 여러 optimzation에 관한 개념들을 알아봤다 그러면 이제 실제로 쓰이는 여러 optimizer에 대해 알아보자

 Optimizer

1. SGD

SGD는 확률적 경사하강법으로, 이 블로그의 포스팅에서 다룬적이 있으니 보고오자

https://roki9914.tistory.com/4

경사하강법과 선형회귀

2. Momentum

현재 batch의 gradient가 이전 batch의 gradient의 방향과 유사할 것이라는 점에 입각하여 해당 batch에서의 gradient만 사용하는 것이 아닌, 이전 batch의 gradient를 일정 계수만큼 반영(보통 0.9)하여 마치 이전 gradient가 관성(momentum)처럼 작용하게 하는 것이다. 이를 통해 각 batch에서 gradient가 요동쳐도 이를 안정화시킬 수 있다는 장점이 있다.

 

3. Nestrov Accelerate gradient(NAG)

현재 batch의 gradient를 이용하여 실제 그 방향으로 전진해보고, 그 지점에서의 gradient를 계산하고 활용해보는 것이다. 이를 통해 local minimum의 좌우를 왕복하는 문제를 해결하고 그 점에 훨씬 빠르게 수렴하게 할 수 있다.

 

4. Adagrad

Neural network가 지금까지 얼마나 변화했는지를 확인하고 많이 변한 parameter는 조금 변화시키고 조금 변한 parameter는 많이 변화시키려는 것이다. 이때, 다음과 같은 식에 기반하여 적용시킨다. 

위 식의 G항이 이전까지의 gradient를 제곱하여 더한 값들로, 이를 분모항에 넣어 g_t 에 해당하는 gradient가 조금 반영되게 하는 것이다. (입실론값은 division by zero를 예방하기 위한 값이다.) 이때의 문제는, train epoch이 커질수록, Gt가 점점 커져서, 뒷부분의 epoch에서는 gradient가 거의 반영되지 않는다는 문제가 있다.

 

5. Adadelta

위의 뒷부분의 epoch에서 gradient가 거의 반영되지 않는 문제를 해결하기 위한 것으로, 정해진 step수(예를 들어 100개) 안에서만의 G항을 계산하여 gradient가 반영되지 않는 것을 막는다. 다만, 이를 위해 정해준 step수 안의 gradient들을 기억해야 하므로, parameter의 수가 너무 많아지면(예를 들어 200만개),  너무 많은 수의 gradient들(2억개)을 기억해야 하는 문제가 있다. 또한, 함수식에 learning rate가 들어있지 않기 때문에 잘 사용되지 않는다.

 

6. RMSprop

RMSprop의 특이한 점이라면 논문을 통해 발표된 것이 아닌, 한 교수가 수업시간에 "내가 이렇게 했더니 잘되더라"라고 말한 것에서 시작된 것이다. RMSprop은 adagrad에서 step size(=learning rate)를 반영한 것이 유일한 차이점이다.

7. Adam

현재 가장 무난한 optimizer로, 지금까지 있었던 adaptive 정보들과, 직전 batch의 momentum을 활용하는 것이 아이디어이다. 각 정보를 어느정도의 계수로 적용해줄지가 관건이다.

지금까지 여러 optimizer에 대해 알아봤다. 마지막으로 여러 Regularization 기법에 대해 알아보자

 

Regularization

Regularization은 generalization을 잘 하기 위한 방법들로, 단적으로 말하면 학습을 방해해 overfitting을 막는 것이다.

 

1. early stopping

말 그대로 모델 학습을 일찍 끝내는 것으로, validation data를 이용해 모델이 overfitting 되기 전에 학습을 중단시키는 것이다.

 

2. Parameter Norm Penalty (aka. weight decay)

Neural Network의 parameter가 너무 커지지 않게 하는 것으로, parameter의 제곱합의 크기를 줄이는 방식으로 parameter의 크기를 조절한다. 이는 수학적으로 증명된 것은 아니지만, 부드러운 형태를 가진 함수일수록 generalization이 잘 될것이라는 가정 하에 사용하는 기법이다.

 

3. data augmentation

데이터의 양이 많을수록 학습이 잘 되기 때문에 이미 주어진 데이터를 살짝식 변형하여 데이터의 양을 늘리는 것이다. 가령 이미지 데이터라면 이미지를 뒤집는다거나 회전시키는 식으로 얻을 수 있고, 문장 데이터라면 동의어로 치환하는 등의 과정을 거칠 수 있다.

그러나, data augmentation은 데이터의 특징에 따라 방법을 고려해야하는 것으로, 가령 x-ray데이터를 augmentation할 때에는 좌우 반전은 괜찮지만 상하 반전을 하는 것은 지양해야 한다.

 

4. Noise robustness

왜 잘되는지에 대해 아직도 의문이 있는 방법으로, data에 noise를 넣으면 학습이 잘 되는 것을 볼 수 있다. 여기에 더해, data뿐만 아니라, 학습중 parameter나 weight에 noise를 넣었을 때도 학습이 잘 되는 것을 볼 수 있다.

5. label smoothing

이것 또한 왜 잘되는지 밝혀진 바가 없는 방법으로, train 단계에서 두 학습 데이터와 label을 섞어서 decision boundary를 smooth하게 만들어주는 방법이다.

6. dropout

neural network의 일부를 0으로 만들어 죽이는 것으로, robust한 data에도 잘 적용되기 때문에 좋은 결과가 나온다는 것이 주된 추측이다.

dropout 전 후 비교

7. batch normalization

이것 또한 왜 잘되는지는 모르나 통계적으로 좋다고 밝혀진 것으로, 적용하고자하는 data의 각 batch를 정규화하는 것이다.

 

지금까지 optimization의 여러 핵심 개념, 실제 사용되는 여러 optimizer들, 그리고 여러 regularization 기법에 대해 알아보았다.